209. 长度最小的子数组

题目

给定一个含有 n 个正整数的数组和一个正整数 **target **。

找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度**。**如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

• 1 <= target <= 109
• 1 <= nums.length <= 105
• 1 <= nums[i] <= 104

---

思路

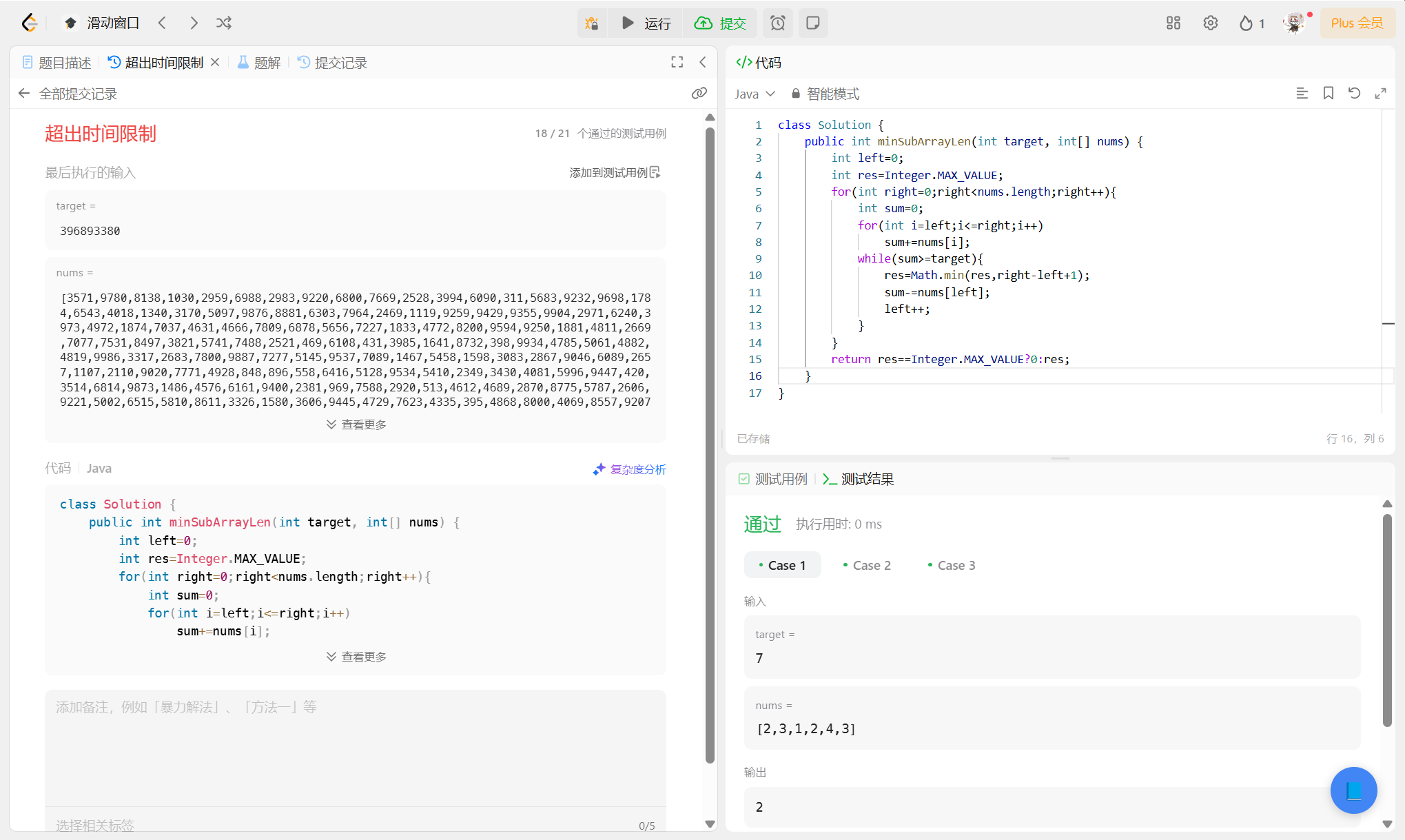
先讲讲还是超时的代码思路

问题回顾

给定一个正整数数组 nums 和一个目标值 target，要求：

• 找出和 ≥ target 的最短连续子数组。
• 返回其长度，如果不存在这样的子数组，返回 0。

---

代码思路

这段代码使用**双指针（left 和 right）**来维护一个滑动窗口，计算窗口内的子数组和，并动态调整窗口大小：

1. 初始化：

   • left = 0（窗口左边界）
   • res = Integer.MAX_VALUE（初始最小长度设为最大值，便于后续比较）

2. 外层循环（right 指针扩展窗口）：

   • right 从 0 开始，逐步向右移动，扩展窗口的右边界。
   • 每移动一次 right，就计算当前窗口 [left, right] 的和 sum。

3. 内层循环（left 指针收缩窗口）：

   • 如果 sum ≥ target，说明当前窗口满足条件：
     • 记录当前窗口长度 right - left + 1，并更新 res（取最小值）。
     • 尝试收缩窗口：left 右移，并减去 nums[left]，继续检查是否仍然满足 sum ≥ target（这一步是为了寻找更小的窗口）。
   • 如果 sum < target，则继续扩展 right。

4. 返回结果：

   • 如果 res 仍然是 Integer.MAX_VALUE，说明没有找到符合条件的子数组，返回 0。
   • 否则返回 res（最小长度）。

---

代码执行示例

以 nums = [2, 3, 1, 2, 4, 3]，target = 7 为例：

right	left	窗口 [left, right]	sum	sum ≥ target?	res 更新
0	0	[2]	2	❌	-
1	0	[2, 3]	5	❌	-
2	0	[2, 3, 1]	6	❌	-
3	0	[2, 3, 1, 2]	8	✔	res = 4
3	1	[3, 1, 2]	6	❌	-
4	1	[3, 1, 2, 4]	10	✔	res = 4
4	2	[1, 2, 4]	7	✔	res = 3
4	3	[2, 4]	6	❌	-
5	3	[2, 4, 3]	9	✔	res = 3
5	4	[4, 3]	7	✔	res = 2
5	5	[3]	3	❌	-

最终 res = 2，即最短子数组 [4, 3]。

---

时间复杂度

• 最坏情况：O(n²)（如果数组是 [1, 1, 1, …, 1]，且 target 很大，每次 right 移动都要重新计算 sum）。
• 优化方法：可以改为前缀和 + 滑动窗口，或者直接维护 sum 变量（减少重复计算），这样能优化到 O(n)。

---

总结

• 优点：代码直观，容易理解，符合滑动窗口的基本思想。
• 缺点：内层循环导致时间复杂度较高，可以进一步优化。
• 适用场景：适用于小规模数据，或对时间要求不严格的情况。

如果希望更高效的解法，可以参考标准滑动窗口（维护 sum 变量，不重复计算），时间复杂度 O(n)。

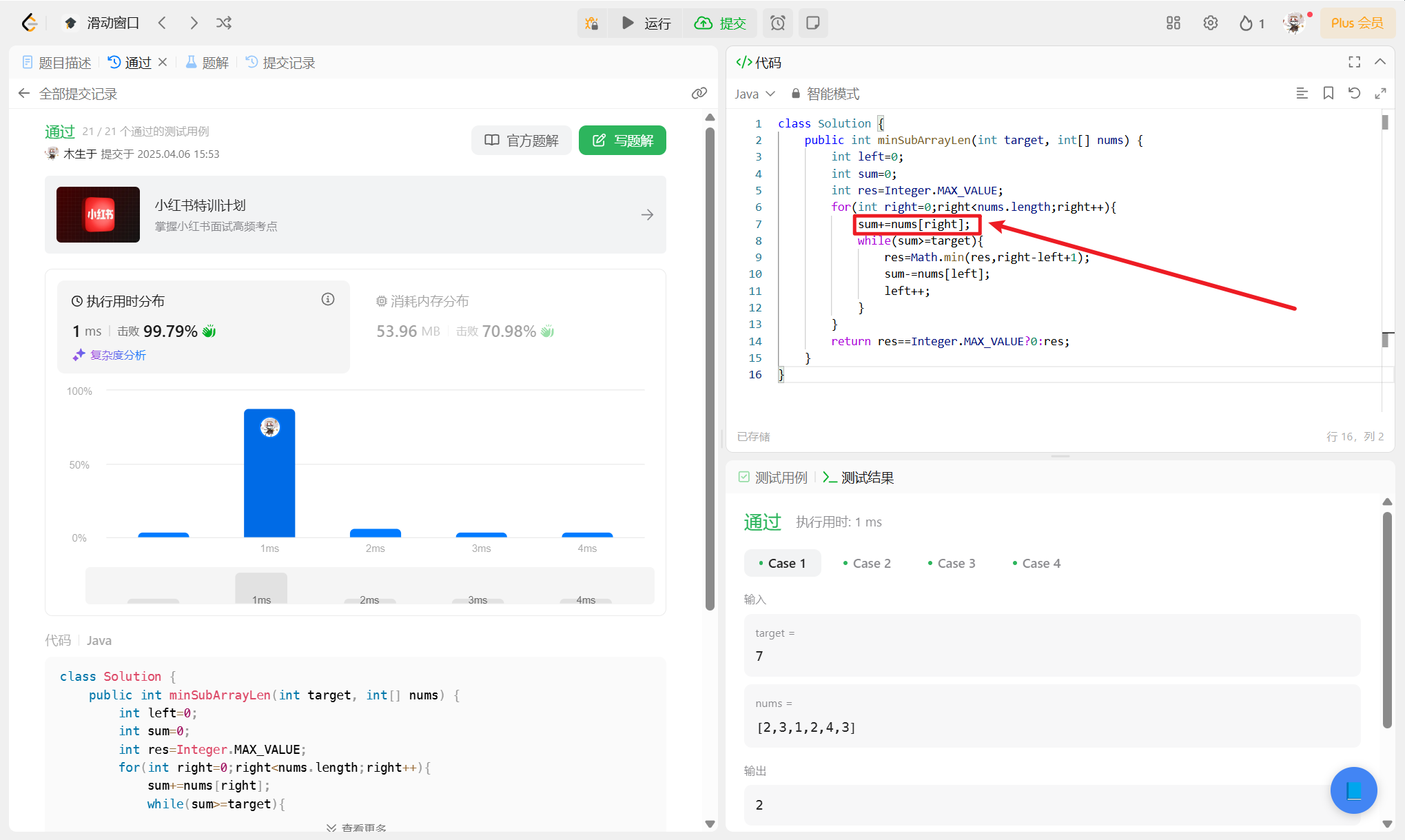
这个思路已经是正确的了，只不过代码有一些累赘，多了一个for循环，将内部的重复计算的for去掉即可！

---

完整代码

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int left=0;
        int sum=0;
        int res=Integer.MAX_VALUE;
        for(int right=0;right<nums.length;right++){
            sum+=nums[right];
            while(sum>=target){
                res=Math.min(res,right-left+1);
                sum-=nums[left];
                left++;
            }
        }
        return res==Integer.MAX_VALUE?0:res;
    }
}